算法导论练习12.2

字数统计: 1.7k阅读时长: 6 min

 2019/08/09  80  Share

12.2-1 假设一棵二叉搜索树中的结点在1到1000之间，现在想要查找值为363得到结点，下面序列那个不是查找过的序列。

a. $2,252,401,398,330,344,397,363$ 。
b. $924,220,911,244,898,258,362,363$ 。
c. $925,202,911,240,912,245,363$ 。
d. $2,399,387,219,266,382,381,278,363$ 。
e. $935,278,347,621,299,392,358,363$ 。

因为这是查找BST过程中的一个序列，因此根据该序列构造BST，如果满足BST的性质，那么就是查找的序列，否则不是。其中c和e不满足。

12.2-2 写出TREE-MINIMUM和TREE-MAXIMUM的递归版本。

//根据书上的版本写的，书中没有判断x是否为空的情况
TREE-MINIMUM(x)
 if x.left == NIL
    return x
 return TREE-MINIMUM(x.left);

TREE-MAXIMUM(x)
 if x.right == NIL
    return x
 return TREE-MAXIMUM(x.right)

12.2-3 写出过程TREE-PREDECESSOR的伪代码

与书上的TREE-SUCCESSOR想对称

TREE-PREDECESSOR
 if x.left != NIL
    return TREE-MAXIMUM(x.left)
 y = x.p
 while y != NIL and y.left == x
    x = y
    y = y.p
return y

12.2-4 Bunyan教授认为他发现了一个二叉搜索树的重要性质。假设在一棵二叉搜索树中查找一个关键字 $k$ ，查找结束于一个树叶。考虑三个集合： $A$ 为查找路径左边的关键字集合； $B$ 为u查找路径上的关键字集合； $C$ 为查找路径右边的关键字集合。Bunyan教授声称： $\forall a \in A,b \in B, c \in C$ ，一定满足 $a \leq b \leq c$ 。请给出该教授这个论断的一个最小可能的反例。

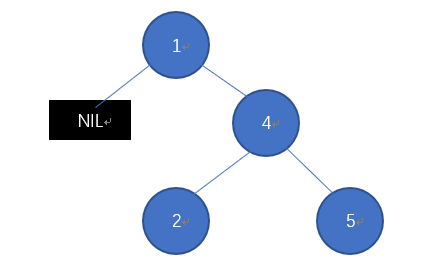
查找5，那么 $B=\{1,4,5\},A=\{2\},C=\{\}$ , 显然不成立。

12.2-5 证明：如果一棵二叉搜索树中一个结点有两个孩子，那么它的后继没有左孩子，它的前驱没有右孩子。

证明：反证法，设结点为 $x$ ，它的前驱为 $pre$ ，那么对于BST的中序遍历序列为 $<\dotsc-pre-x-\dotsc>$ ，假如 $pre$ 存在右孩子 $ppret$ ，那么在中序遍历时，遍历完成 $pre$ 后接着遍历 $ppre$ ，这与之前中序遍历的序列相矛盾。即 $x$ 的前驱 $pre$ 不存在右孩子。同理 $x$ 的后继结点不存在左孩子。

12.2-6 考虑一棵二叉搜索树 $T$ ，其关键字互不相同。证明：如果 $T$ 中一个结点 $x$ 的右子树为空，且 $x$ 有一个后继 $y$ ，那么 $y$ 一定是 $x$ 的最底层的祖先，并且左孩子也是 $x$ 的祖先。（注意到，每个结点都是它自己的祖先。）

证明：
首先确定 $y$ 是 $x$ 的祖先，如果 $y$ 不是 $x$ 的祖先，设 $x,y$ 的第一个共同祖先为 $z$ ，那么根据BST的性质有， $x < z < y$ （因为x没有右子树，那么y只能存在于z的右子树，而x存在于z的左子树，否则就无法满足y为x后继即 x<y的关系），那么 $x$ 的后继不再是 $y$ ，因此假设不成立。 $y$ 为 $x$ 的祖先得证。
接下来证明 $y.left$ 是 $x$ 的祖先。假设 $y.left$ 不是 $x$ 的祖先，那么 $y.right$ 将是 $x$ 的祖先，意味着 $x > y$ ，矛盾。因此 $y.left$ 是 $x$ 的祖先。
最后证明 $y$ 是 $x$ 的最底层祖先，同时 $y.left$ 也是 $x$ 的祖先。假设 $y$ 不是 $x$ 的最底层祖先但是 $y.left$ 是 $x$ 的祖先，令 $z$ 表示最底层祖先， $z$ 一定是 $y$ 的左子树，因此有 $z < y$ ，意味着 $z$ 是 $x$ 的后继，矛盾，假设不成立。

12.2-7 对于一棵有 $n$ 个结点的二叉搜索树，有另一个方法实现中序遍历，先调用TREE-MINUMUM找到这棵树中的最小元素，然后再调用n-1次的TREE-SUCCESSOR。证明：该算法的时间复杂度为 $\Theta(n)$ 。

证明：我们要想证明这个边界，其实不难实现，可以通过再TREE-MINIMUM和TREE-SUCCESSOR中统计访问边的次数，对于BST是树，因此满足边的次数=顶点数-1。不难发现每条边访问次数不超过两次，同时每个顶点需要访问依次，因此时间复杂度为 $\Theta(n)$

下面证明对于每一条边最多访问两次：一次从下降（从高到低），一次上升（从低到高）

考虑在树中的一个点 $u$ ,还有它的孩子 $v$ 。我们需要先访问从 $(u,v)$ ，才能访问 $(v,u)$ 。对于下降，只有出现在TREE-MINIMUM，对于上升，只有出现在TREE-SUCCRSSOR并且该结点没有右孩子。

假设 $v$ 是 $u$ 的左孩子

在打印 $u$ 之前，我们需要打印 $u$ 的左子树，保证下降的遍历边 $(u,v)$
$v$ 为根的左子树遍历完成后，打印 $u$ 。从 $v$ 为根的左子树的最大结点,调用TREE-SUCCESSOR中，上升遍历边(u,v)。当 $u$ 的左子树遍历完成后，边 $(u,v)$ 不再访问。

假设 $v$ 是 $u$ 的右孩子

当 $u$ 打印后，TREE-SUCCESSOR(u)被调用，为了访问 $v$ 为根的右子树的最小元素，需要下降的遍历边 $(u,v)$ 。

当 $u$ 的右子树遍历完成后， $v$ 为根的右子树的最大结点，调用的TREE-SUCCRSSOR，上升遍历边 $(u,v)$ 。当 $u$ 的右子树遍历完成后，边 $(u,v)$ 不再访问。

因此，每条边访问次数不会超过2次。时间复杂度为 $\Theta(n)$

12.2-8 证明：在一棵高度为 $h$ 的二叉搜索树中，不论从哪个结点开始， $k$ 次连续的TREE-SUCCESSOR调用所需时间为 $\Theta(k+h)$ 。

我们记调用TREE-SUCCESSOR的结点为 $x$ ，令 $y$ 为 $x$ 的第 $k$ 个后继结点, $z$ 为 $x,y$ 的最底层公共祖先。连续调用TREE-SUCCESSOR类似树的遍历，每条边的遍历次数不超过2次，所以我们不会检查一个结点超过3次。另外，任何结点关键字不是在 $x,y$ 之间最多检查一次，发生在一条从$ $或$ $(路径)。这些路径的长度由$ y $限制,因此最坏情况时间复杂度为$ 3k+2h=O(k+h)$。

12.2-9 设 $T$ 是一颗二叉搜索树，其关键字互不相同；设 $x$ 是一个叶结点， $y$ 为其父结点。证明： $y.key$ 或者 $T$ 树中大于 $x.key$ 的最小关键字，或者是 $T$ 树中小于 $x.key$ 的最大关键字。

证明：假设 $x$ 是 $y$ 的左孩子，那么 $x$ 的后继是 $y$ ，即 $y.key$ 是 $T$ 树种大于 $x.key$ 的最小关键字，若 $x$ 是 $y$ 的右孩子，那么 $y$ 的前驱是 $x$ ，即 $y.key$ 是 $T$ 树小于 $x.key$ 的最大关键字。

原文作者：007havegone

原文链接：http://007havegone.github.io/2019/08/09/算法导论练习12-2/

发表日期：August 9th 2019, 1:22:44 am

更新日期：August 12th 2019, 4:18:11 pm

Next Post

算法导论练习12.3
Previous Post

算法导论练习12.1

CATALOG

